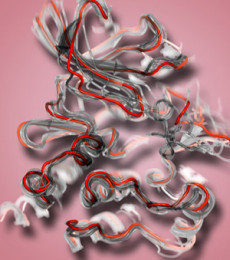
Protein Dynamics Hit the Big Screen

Scientists from Berkeley Lab and UC Berkeley are using one the world's most powerful computers to simulate how protein molecules move, rotate, and fold as they carry out life's most fundamental tasks. Although they only approximate real-life phenomena, the increasingly realistic movies are becoming useful complements to real-world experiments in helping scientists determine how proteins function. Using them, biologists can gain a better understanding of how incorrectly folded proteins lead to a range of diseases, or how other proteins synthesize adenosine triphosphate (ATP), the fuel that powers many biomolecular motors.

"Proteins are very complex molecules with thousands of atoms, but they don't come with a user's manual," says John Kuriyan of Berkeley Lab's Physical Biosciences Division. "Fortunately, over the past few years, rapid increases in computing power and better simulation programs have made it possible to visualize protein dynamics like never before."

The simulations are created at the National Energy Research Scientific Computing Center (NERSC), which is located at Berkeley Lab and is the flagship scientific computing facility for DOE's Office of Science. NERSC boasts the raw power needed to develop simulations that are detailed enough to capture a protein's fastest movement and long enough to portray their relatively infrequent but biologically important changes. In some cases, this means stringing together femtosecond-length, atom-scale snapshots of a 50,000-atom protein, frame by frame, into movies that span several nanoseconds (a femtosecond is one-millionth of a nanosecond, and a nanosecond is one-billionth of a second).

Although these high-resolution simulations take days to prepare even on a supercomputer, they enable Kuriyan and colleagues to test-drive proteins under a variety of conditions. They can see what happen when a protein is given just enough energy to teeter on the edge of a conformational change. Or they can prod a protein to change shape, and gauge how forcefully it resists or how readily it gives in.

"The simulations allow us to push here and there and determine how the protein responds," says Kuriyan, who is also a Howard Hughes Medical Institute investigator and a Chancellor's Professor in UC Berkeley's Department of Molecular and Cell Biology and Department of Chemistry. "This is important because it isn't always obvious which experiments will address a protein's mechanistic properties."

Berkeley Lab researchers aren't the only scientists spearheading the development of these virtual protein movies, but they're uniquely suited to lead the way. Along with NERSC, Berkeley Lab and UC Berkeley have joint appointees, like theoretical chemists David Chandler and Phillip Geissler, who are constantly refining the fundamental molecular theories on which the simulations are based. Add the expertise of experimental biologists like Kuriyan, who put real proteins through the wringer to learn how they work, and the Lab has an ideal blend of theory, practical know-how, and computing power to create almost lifelike movies.

So far, Kuriyan and colleagues have used NERSC simulations to learn how certain proteins, called Src tyrosine kinases, transmit signals initiated by growth factor receptors in human cells. Mutant forms of these proteins can trigger cancer. They've also simulated the conformational and energy changes that proteins involved in DNA replication must undergo in order to rapidly copy DNA strands.

In each case, the simulations furthered their understanding of protein dynamics and helped guide real-world experiments. They also underscored the need for powerful computers. The quickest motion in a protein is the stretch of the carbon-hydrogen bond, which occurs in about one femtosecond. This means that each frame of a simulation must depict a protein's movement femtosecond by femtosecond. If it doesn't, the simulation will skip over these carbon-hydrogen stretches and be as true to life as a jerky 1920s movie. But interesting changes in proteins, such as the rotation of a portion of the ATP-making enzyme, often occur in the microsecond to millisecond time scale — up to nine orders of scale slower than a femtosecond. In other words, a simulation must weave together billions of femtosecond-length snapshots in order to capture one or two rare but important changes.

The dilemma is like filming the muscular movements of a person. To capture the smallest muscle twitch, down to a single heartbeat, the film must have several frames per second. Unfortunately, the person might not do something significant, like go skydiving, for days. The filmmaker must churn through miles of film reel in order to record that infrequent but important leap from an airplane.

"This is why computer speed becomes very important. The faster the computer can simulate each frame of the movie, the more frames can be generated, and the sooner we will get to something interesting," says Kuriyan.

He adds that the simulations aren't perfect. They're constructed frame by frame, so no matter how fast they become, they will always gloss over some nuance of a protein's motion. In addition, a ten-nanosecond simulation of a large protein molecule sometimes requires 20 to 40 days of a supercomputer's processor time to create.

"We'd like to run a simulation and get the answer in a day so we can change what we are doing in the lab," says Kuriyan. "We're not close to being there yet. But increases in computer speed have enabled dramatic advances recently, and this trend will continue. It is very important to support national resources like NERSC that help maintain competitiveness and very fast computation."

Kuriyan and Martin Karplus of Harvard University discuss the promise of protein molecule simulations in a paper entitled "Molecular dynamics and protein function," which was published online May 3, 2005 by the Proceedings of the National Academy of Sciences.

• More about John Kuriyan's research
• More about Kuriyan's work on DNA's Grand Prix
• Read the Karplus and Kuriyan paper in PNAS (pdf)